Java 集合

概述

Java 集合可分为 Collection 和 Map 两大体系：

  • Collection接口：用于存储一个一个的数据，也称单列数据集合。
    • List子接口：用来存储有序的、可以重复的数据（主要用来替换数组，"动态"数组）
      • 实现类：ArrayList(主要实现类)、LinkedList、Vector
    • Set子接口：用来存储无序的、不可重复的数据（类似于高中讲的"集合"）
      • 实现类：HashSet(主要实现类)、LinkedHashSet、TreeSet
  • Map接口：用于存储具有映射关系“key-value对”的集合，即一对一对的数据，也称双列数据集合。(类似于高中的函数、映射。(x1,y1),(x2,y2) ---> y = f(x) )
    • HashMap(主要实现类)、LinkedHashMap、TreeMap、Hashtable、Properties
  • JDK提供的集合API位于java.util包内

整体框架图

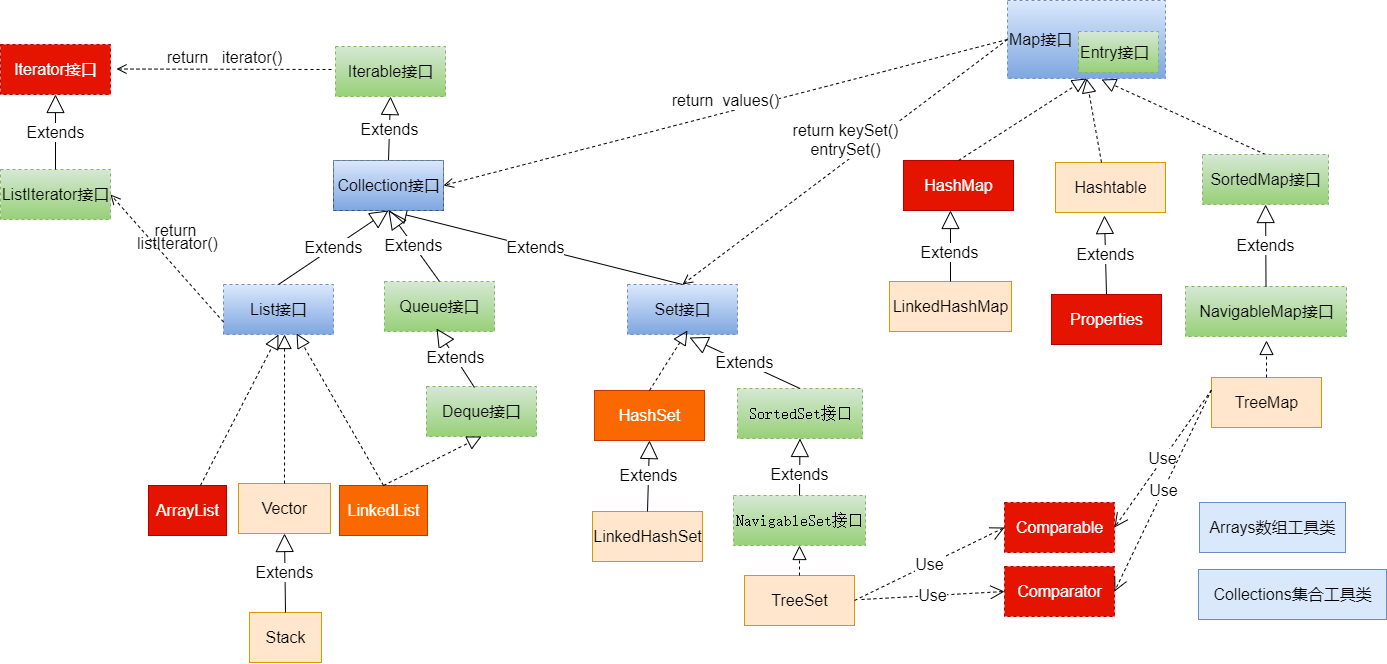
集合框架全图.png

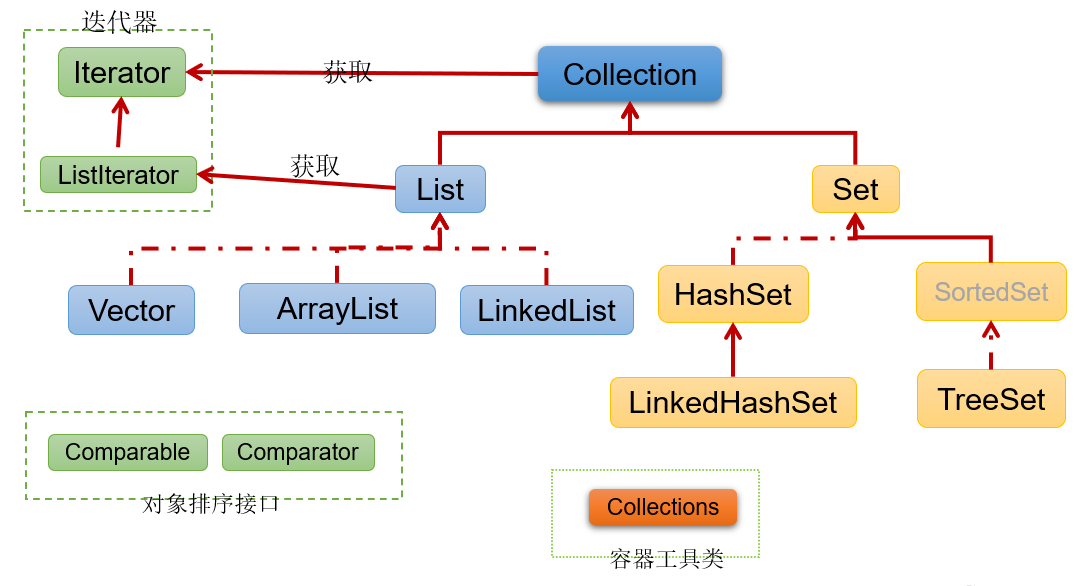
简图

image-20220407203244029.png

ArrayList

1.概况

  1. 底层基于数组结构
  2. 有序,可重复
  3. 线程不安全

2.算法逻辑

jdk 1.7.0_04中

  1. 当new ArrayList()时,初始化一个长度为10的Object数组Object[10]
  2. 调用add()方法时,首先判断是否需要扩容
    • 不需要扩容: 将下标对应的槽赋值
    • 需要扩容(例如第11个元素): 创建一个当前容量1.5倍的数组,然后将老数组拷贝进新数组

jdk 1.8.0之后

  1. 当new ArrayList()时,初始化一个长度为0的Object数组Object[]{}
  2. 第一次调用add()方法时,初始化数组长度为10,将下标对应的槽赋值
  3. 后续调用时,首先判断是否需要扩容
    • 不需要扩容: 将下标对应的槽赋值
    • 需要扩容(例如第11个元素): 创建一个当前容量1.5倍的数组,然后将老数组拷贝进新数组

Vector

1.概况

  1. 底层基于数组结构
  2. 有序可重复
  3. 线程安全

2.算法逻辑

  1. 当new Vector()时,初始化一个长度为10的Object数组Object[10]
  2. 调用add()方法时,首先判断是否需要扩容
    • 不需要扩容: 将下标对应的槽赋值
    • 需要扩容(例如第11个元素): 创建一个当前容量2倍的数组,然后将老数组拷贝进新数组
  • 与1.7相比只是多了初始化容量

LinkedList

1.概况

  1. 底层基于双向链表结构（不需要扩容）
  2. 线程不安全
  3. 有序可重复

2.算法逻辑

  1. 当new LinkedList()时,构造器没有执行任何操作，但是LinkedList实例初始化了一些Node对象。
//定义上一个节点对象
transient Node<E> first;
//定义下一个节点对象
transient Node<E> last;

//静态内部类Node
private static class Node<E> {
      E item;
      Node<E> next;
      Node<E> prev;

      Node(Node<E> prev, E element, Node<E> next) {
          this.item = element;
          this.next = next;
          this.prev = prev;
        }
    }
  1. 调用add()方法时:
  • add方法源码
void linkLast(E e) {
      final Node<E> l = last;
      final Node<E> newNode = new Node<>(l, e, null);
      last = newNode;
      //此处注意l和last不是同一地址值
      if (l == null)
          first = newNode;
      else
          l.next = newNode;
      size++;
      modCount++;
    }
  • 执行流程
//第一次调用：
     final Node<E> l = null;
     final Node<E> newNode = new Node<>(l, "AA", null);
     last = newNode;
     first = newNode;
     
     //最终结果
     Node<E> first = new Node<>(null, "AA", null);
     Node<E> last = new Node<>(null, "AA", null);
//后续调用：
    final Node<E> l(0xaa) = new Node<>(null, "AA", null);
    
    //BB节点的prev指向整个AA的Node节点
    final Node<E> newNode(0xbb) = new Node<>(0xaa, "BB", null);
    
    //last = new Node<>(0xaa, "BB", null);
    last = newNode;
    
    //AA节点的next指向整个BB的Node节点l(0xaa) = new Node<>(null, "AA", 0xbb);
    l.next = newNode;
    //最终结果
    Node<E> first(0xaa) = new Node<>(null, "AA", 0xbb);
    Node<E> last(oxbb) = new Node<>(0xaa, "BB", null);

HashMap

1.概况

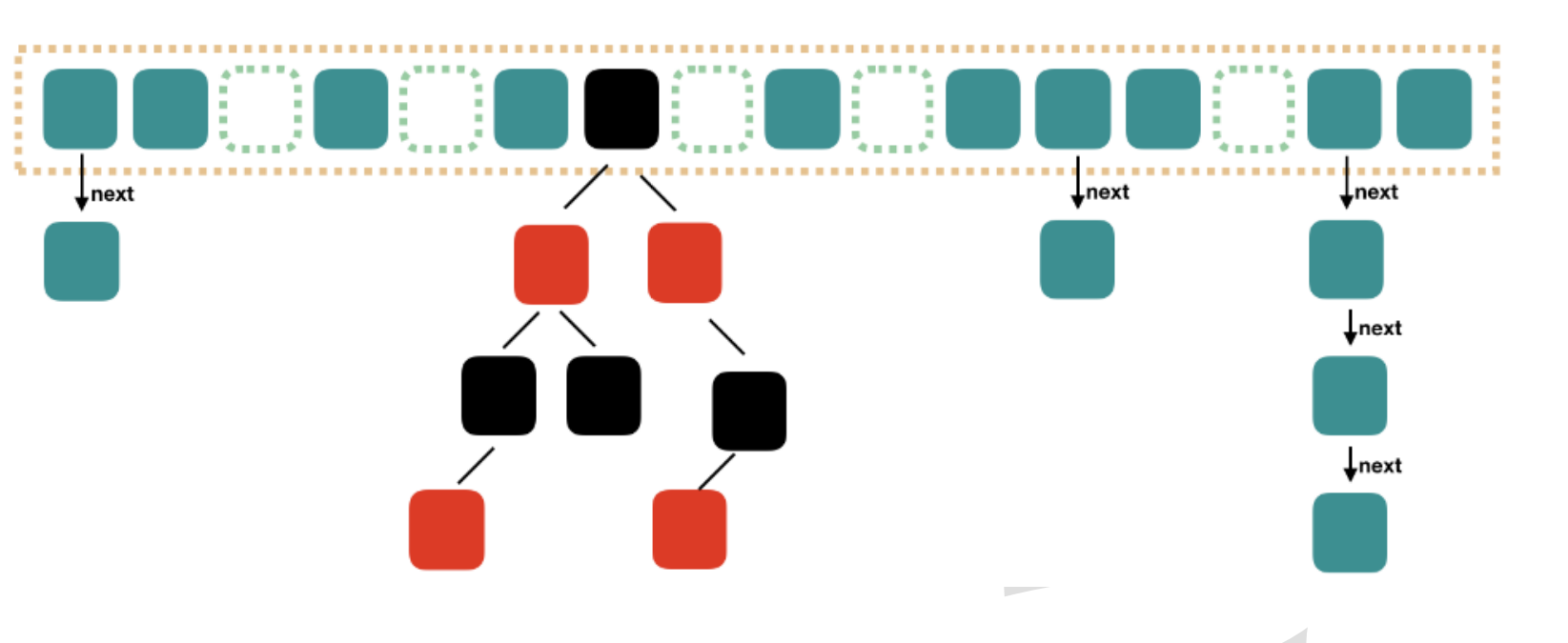
  1. 存储数据采用的哈希表结构，底层使用一维数组+单向链表+红黑树进行key-value数据的存储
  2. HashMap是线程不安全的
  3. 允许添加 null 键和 null 值。
  4. HashMap 判断两个key相等的标准是：两个 key 的hashCode值相等，通过 equals() 方法返回 true。
  5. HashMap 判断两个value相等的标准是：两个 value 通过 equals() 方法返回 true。
  6. HashMap(int initialCapacity)构造器的initialCapacity不是初始容量，是2的整数次幂，例如传3，实际容量为4，传1->1,8->8,15->16

2.算法逻辑

1.7与1.8中的不同点

  1. 底层数据结构

    • 1.7中底层使用一维数组+单向链表数据结构
    • 1.8中底层使用一维数组+单向链表+红黑树进行key-value数据的存储

  2. 链表结构新增/移除节点时

    • 1.7中采用头插法
    • 1.8中采用尾插法
    • 1.8中当链表长度大于8并且数组长度达到64时,会将数据结构转变为红黑树，当长度小于6时会再次将数据结构转变为链表结构

  3. 创建实例对象时

    • 1.7中new HashMap()时，底层会初始化一个Entry<K,V>[] table = new Entry<>[16]数组;
    • 1.8中new HashMap()时，底层只初始化了一个loadFactor = 16，当调用put()方法时，才去初始化一个Node<K,V>[] table = new Node<>[]();

底层算法

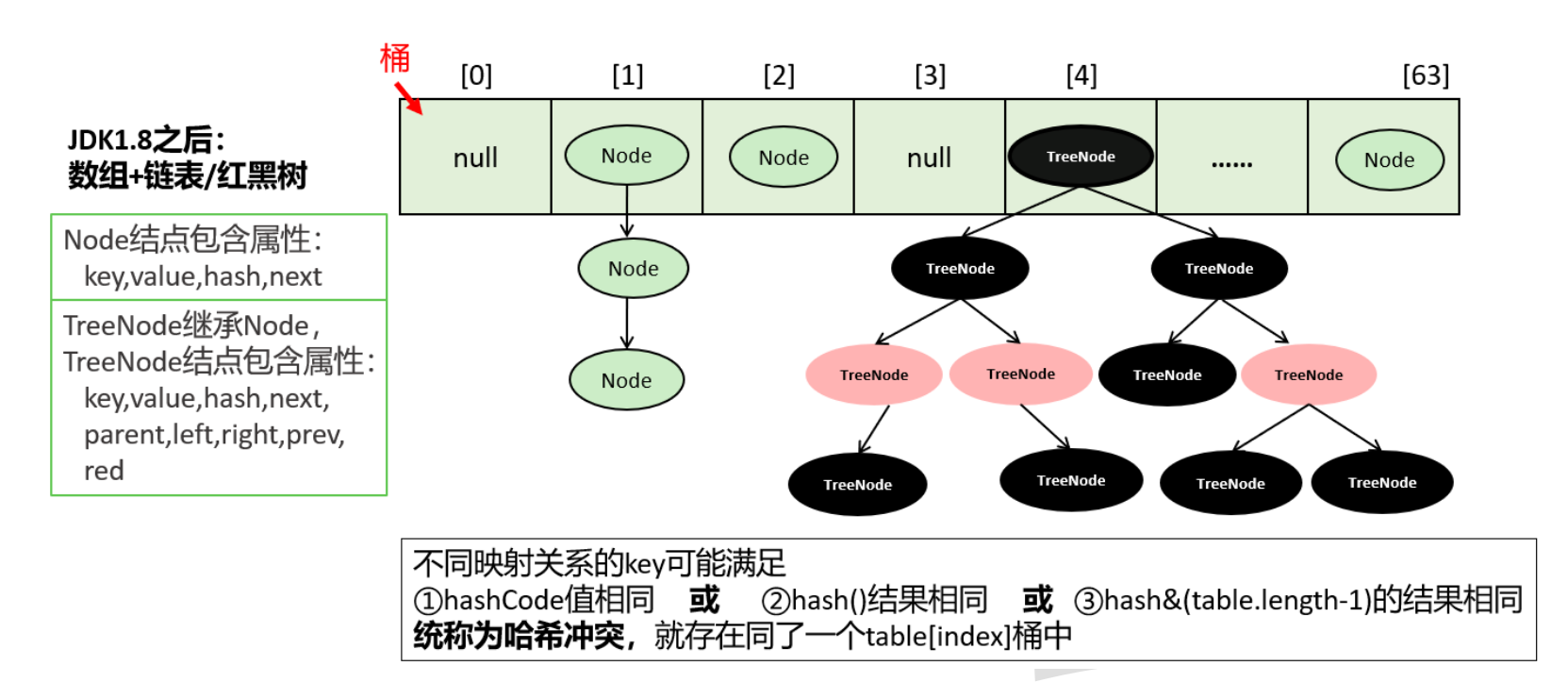
hashmap1.png hashmap.png

  1. new HashMap()时，初始化loadFactor = 16

  2. 执行put(key,value)时

    1. 将key通过调用hash()方法，过程中调用key的hashCode()方法，然后经过计算得到hashKey1
    2. Node<K,V>[] table如果没有初始化，初始化table长度
    3. 通过hashKey1计算出下标[i]，如果该下标没有值，则将元素添加到该下标位置
    4. 如果计算的下标[i]位置上有值，则比较该位置的hashKey2与hashKey1是否相同，使用key的equal()再次两者是否相同，相同的话执行修改操作
    5. 如果不相同，比较单向链表的下个元素，如果都不相同，则将元素放在最后元素后面
    6. 如果该下标的元素数量超过8，会将单向链表结构转化为红黑树结构存储

知识点补充：红黑树

红黑树：是一种平衡二叉查找树的变体，它的左右子树高差有可能大于 1，所以红黑树不是严格意义上的平衡二叉树（AVL），但 对之进行平衡的代价较低， 其平均统计性能要强于 AVL 。 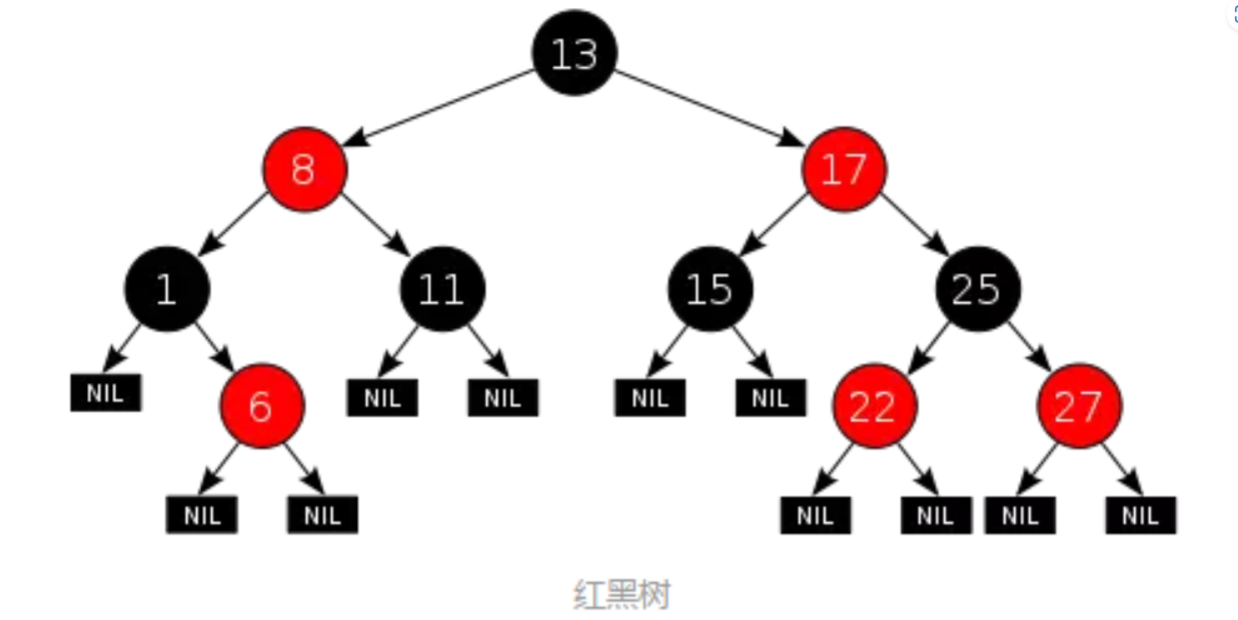红黑树.png 红黑树是每个结点都带有颜色属性的二叉查找树，颜色或红色或黑色。 在二叉查找树强制一般要求以外，对于任何有效的红黑树我们增加了如下的额外要求:

  • 结点是红色或黑色
  • 根结点是黑色
  • 所有叶子都是黑色。（叶子是NIL结点）
  • 每个红色结点的两个子结点都是黑色。（从每个叶子到根的所有路径上不能有两个连续的红色结点）
  • 从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点。

与 AVL 树相比，红黑树的查询效率会有所下降，这是因为树的平衡性变差，高度更高。但红黑树的删除效率大大提高了，因为红黑树同时引入了颜色，当插入或删除数据时，只需要进行 O(1)次数的旋转以及变色就能保证基本的平衡，不需要像 AVL 树进行 O(lgn)次数的旋转。总的来说， 红黑树的统计性能高于 AVL。

对于数据在内存中的情况（如上述的 TreeMap 和 HashMap），红黑树的表现是非常优异的。但是对于数据在磁盘等辅助存储设备中的情况（如 MySQL 等数据库），红黑树并不擅长，因为红黑树长得还是太高了。当数据在磁盘中时，磁盘 IO 会成为最大的性能瓶颈，设计的目标应该是尽量减少 IO 次数；而树的高度越高，增删改查所需要的 IO 次数也越多，会严重影响性能。

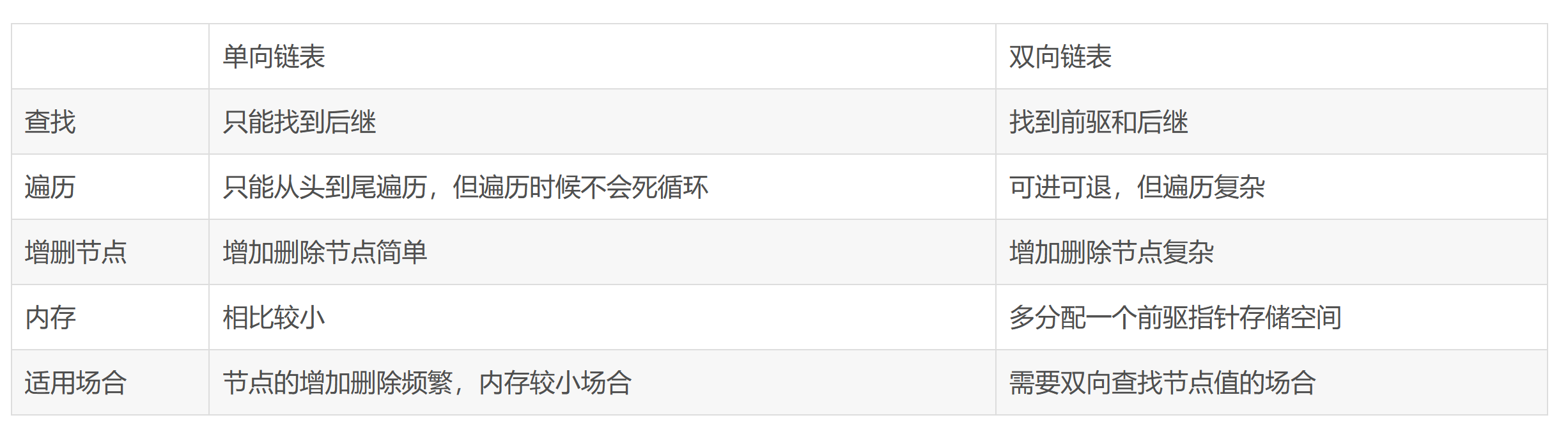
单向链表和双向链表

单向链表和双向链表.png